798. Платформы

В старых играх следующая ситуация встречается довольно часто. Герой прыгает по платформам, висящим в воздухе. Он должен перебраться от одного края экрана до другого. При прыжке с одной платформы на соседнюю, герой тратит |y₂ – y₁| энергии, где y₁ и y₂ – высоты соответствующих платформ. Кроме того, есть суперприём, позволяющий перескочить через платформу, но на это затрачивается 3 · |y₃ – y₁| единиц энергии.

Известны высоты платформ в порядке от левого края до правого. Найдите минимальное количество энергии, достаточное, чтобы добраться с 1-й платформы до n-й (последней), и список (последовательность) платформ, по которым нужно пройти.

Вход. Первая строка содержит количество платформ n (2 ≤ n ≤ 10⁵). Вторая строка содержит n целых чисел, значения которых не превышают по модулю 4000 – высоты платформ.

Выход. В первой строке выведите минимальное количество энергии. Во второй строке выведите количество платформ, по которым нужно пройти. В третьей строке выведите список этих платформ.

Пример входа 1	Пример выхода 1
4 1 2 3 30	29 4 1 2 3 4
Пример входа 2	Пример выхода 2
6 4 6 15 5 10 12	12 5 1 2 4 5 6

РЕШЕНИЕ

динамическое программирование

Анализ алгоритма

Пусть e[i] содержит минимальное количество энергии, необходимое для того, чтобы добраться с 1-й платформы до i-ой. Очевидно, что e[1] = 0 (добраться с первой платформы до первой не требует расхода энергии), а e[2] = |y₂ – y₁|, так как на вторую платформу можно попасть только с первой.

В ячейке p[i] будем хранить номер платформы, с которой совершен прыжок на i-ую. Изначально положим p[1] = -1 (начальная первая платформа), а также p[2] = 1.

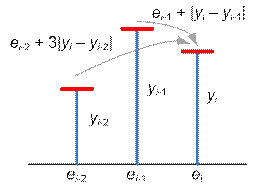
На i-ую платформу (i ≥ 3) возможны два варианта прыжка:

· либо с (i – 1)-ой, затратив e[i – 1] + |y_i – y_i-1| энергии,

· либо с (i – 2)-ой, совершив суперприем и затратив e[i – 2] + 3·|y_i – y_i-2| энергии.

Отсюда

e[i] = min( e[i – 1] + |y_i – y_i-1| , e[i – 2] + 3·|y_i – y_i-2| )

Если прыжок на i-ую платформу совершается с (i – 1)-ой, то устанавливаем p[i] = i – 1. Если с (i – 2)-ой, то положим p[i] = i – 2. Для нахождения количества платформ, по которым совершались прыжки с первой до n-ой, следует пройтись с n-ой платформы до первой двигаясь каждый раз с i-ой платформы на p[i]-ую.

Пример

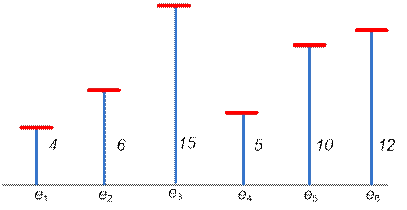
Рассмотрим второй пример. Имеются 6 платформ с заданными высотами.

Вычисляем затраченные энергии при прыжках:

· e[1] = 0, p[1] = -1;

· e[2] = |6 – 4| = 2, p[2] = 1;

· e[3] = min(e[2] + |15 – 6|, e[1] + 3 * |15 – 4|) = min(11, 33) = 11, p[3] = 2;

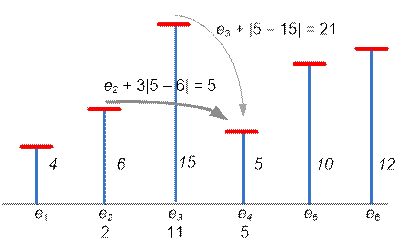
· e[4] = min(e[3] + |5 – 15|, e[2] + 3 * |5 – 6|) = min(21, 5) = 5, p[4] = 2;

· e[5] = min(e[4] + |10 – 5|, e[3] + 3 * |10 – 15|) = min(10, 26) = 10, p[5] = 4;

· e[6] = min(e[5] + |12 – 10|, e[4] + 3 * |12 – 5|) = min(12, 26) = 12, p[6] = 5;

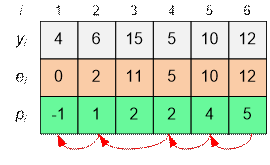
Для восстановления пути следует двигаться с конечной (6-ой) платформы назад по указателям p[i]:

Список платформ, по которым следует пройти, будет следующим:

1, 2, 4, 5, 6

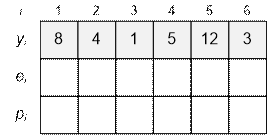
Упражнение

Заполните массивы для следующих входных данных.

Реализация алгоритма

Объявим необходимые массивы.

#define MAX 100001

int y[MAX], e[MAX], p[MAX], res[MAX];

Читаем входные данные.

scanf("%d",&n);

for(i = 1; i <= n; i++) scanf("%d",&y[i]);

Устанавливаем начальные значения ячеек массивов.

e[1] = 0; e[2] = abs(y[2] - y[1]);

p[1] = -1; p[2] = 1;

В цикле вычисляем значения ячеек e[i] и p[i] (3 ≤ i ≤ n), сравнивая значения e[i – 1] + |y_i – y_i-1| и e[i – 2] + 3*|y_i – y_i-2|.

for(i = 3; i <= n; i++)

{

a = e[i-1] + abs(y[i] - y[i-1]);

b = e[i-2] + 3 * abs(y[i] - y[i-2]);

if (a < b)

{

e[i] = a; p[i] = i - 1;

} else

{

e[i] = b; p[i] = i - 2;

}

}

В переменной ptr вычисляем количество платформ, по которым следует пройти. При этом на платформу i необходимо прыгать с платформы p[i].

ptr = 0;

for(i = n; i > 0; i = p[i])

res[ptr++] = i;

Минимальное количество энергии, необходимое для достижения n-ой платформы с первой, равно e[n]. Количество пройденных платформ равно ptr.

printf("%d\n%d\n",e[n],ptr);

Выводим список номеров платформ.

for(i = ptr - 1; i >= 0; i--)

printf("%d ",res[i]);

printf("\n");

Java реализация

import java.util.*;

public class Main

{

public static int MAX = 100001;

static int y[] = new int[MAX];

static int e[] = new int[MAX];

static int p[] = new int[MAX];

static int res[] = new int[MAX];

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

int n = con.nextInt();

for(int i = 1; i <= n; i++)

y[i] = con.nextInt();

e[1] = 0; e[2] = Math.abs(y[2] - y[1]);

p[1] = -1; p[2] = 1;

for(int i = 3; i <= n; i++)

{

int a = e[i-1] + Math.abs(y[i] - y[i-1]);

int b = e[i-2] + 3 * Math.abs(y[i] - y[i-2]);

if (a < b)

{

e[i] = a; p[i] = i - 1;

} else

{

e[i] = b; p[i] = i - 2;

}

}

int ptr = 0;

for(int i = n; i > 0; i = p[i])

res[ptr++] = i;

System.out.println(e[n] + "\n" + ptr);

for(int i = ptr - 1; i >= 0; i--)

System.out.print(res[i] + " ");

System.out.println();

con.close();

}

}

Python реализация

Читаем входные данные.

 
n = int(input())
y = [0] + list(map(int, input().split()))
 

Инициализируем списки.

 
e = [0] * (n + 1)
p = [0] * (n + 1)
 

Устанавливаем начальные значения ячеек.

 
e[1], e[2] = 0, abs(y[2] - y[1])
p[1], p[2] = -1, 1
 

В цикле вычисляем значения ячеек e[i] и p[i] (3 ≤ i ≤ n), сравнивая значения e[i – 1] + |y_i – y_i-1| и e[i – 2] + 3*|y_i – y_i-2|.

 
for i in range(3, n+1):
 a = e[i - 1] + abs(y[i] - y[i - 1])
 b = e[i - 2] + 3 * abs(y[i] - y[i - 2])
 if a < b: e[i], p[i] = a, i - 1
 else: e[i], p[i] = b, i - 2
 

В списке res сохраняем платформы, по которым следует пройти. При этом на платформу i следует необходимо с платформы p[i].

 
res = []
i = n
while i > 0:
 res.append(i)
 i = p[i]
 

Минимальное количество энергии, необходимое для достижения n-ой платформы с первой, равно e[n]. Количество пройденных платформ равно ptr.

 
print(e[-1])
print(len(res))
 

Выводим список номеров платформ. Список res следует вывести в обратном порядке.

 
print(*res[::-1])